ARDEN'S THEOREM FOR REGULAR EXPRESSIONS

-
Image
    Identities for Regular Expression:- Given R, P, L, Q as regular expressions, the following identities hold − ∅* = ε ε* = ε RR* = R*R R*R* = R* (R*)* = R* RR* = R*R (PQ)*P =P(QP)* (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)* R + ∅ = ∅ + R = R   (The identity for union) R ε = ε R = R   (The identity for concatenation) ∅ L = L ∅ = ∅   (The annihilator for concatenation) R + R = R   (Idempotent law) L (M + N) = LM + LN   (Left distributive law) (M + N) L = ML + NL   (Right distributive law) ε + RR* = ε + R*R = R* Arden's Theorem:- In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions. Statement  − Let  P  and  Q  be two regular expressions. If  P  does not contain null string, then  R = Q + RP  has a unique solution that is  R = QP* Proof  − R = Q + (Q + RP)P  [After putting the value R = Q + RP] = Q + ...
Post a Comment

NON-DETERMINISTIC FINITE AUTOMATA (N.D.F.A.)

-
 About N.D.F.A :-
-->A nondeterministic finite automaton (NFA), or nondeterministic finite-state machine, does not need to obey these restrictions. In particular, every DFA is also an NFA. Sometimes the term NFA is used in a narrower sense, referring to an NFA that is not a DFA, but not in this article.
Using the subset construction algorithm, each NFA can be translated to an equivalent DFA; i.e., a DFA recognizing the same formal language. Like DFAs, NFAs only recognize regular languages.
NFAs were introduced in 1959 by Michael O. Rabin and Dana Scott, who also showed their equivalence to DFAs. NFAs are used in the implementation of regular expressions: Thompson's construction is an algorithm for compiling a regular expression to an NFA that can efficiently perform pattern matching on strings. Conversely, Kleene's algorithm can be used to convert an NFA into a regular expression (whose size is generally exponential in the input automaton)
-->The finite automata are called NFA when there exist many paths for specific input from the current state to the next state. Every NFA is not DFA, but each NFA can be translated into DFA. NFA is defined in the same way as DFA but with the following two exceptions, it contains multiple next states, and it contains ε transition.
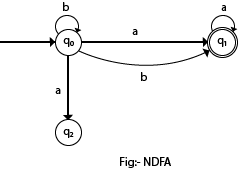
-->In the following image, we can see that from state q0 for input a, there are two next states q1 and q2, similarly, from q0 for input b, the next states are q0 and q1. Thus it is not fixed or determined that with a particular input where to go next. Hence this FA is called non-deterministic finite automata.
Non-Deterministic finite automata
->NFA also has five states same as DFA, but with different transition function, as shown follows:
δ : Q x ∑ →2Q
where,
Q: finite set of states  
∑: finite set of the input symbol  
q0: initial state   
F: final state  
δ: Transition function
--> An NFA can be represented by digraphs called state diagram. In which:
-The state is represented by vertices.
-The arc labeled with an input character show the transitions.
-The initial state is marked with an arrow.
-The final state is denoted by the double circle.
Examples:-
1. NDFA with ∑ = {0, 1} accepts all strings with 01.
-->

Non-Deterministic finite automata
Since the condition here is that it accepts the string starts with '01'. No dead state will  denote here for the undesirable string condition.
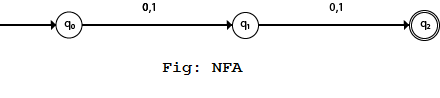
2. NDFA with ∑ = {0, 1} and accept all string of length atleast 2
-->

Non-Deterministic finite automata
Since it accepts only the string of length 2, so there is no self loop and also not any dead state will be drawn for any undesirable condition.
3. Design an NFA with ∑ = {0, 1} accepts all string ending with 01.
--> 

Examples of NFA
Since at last of the string there must be 01 no matter what the stream of input symbol are behind '01'.

Comments

Post a Comment

Popular posts from this blog

EQUIVALENCE OF TWO FINITE AUTOMATAs

-
Image
An Automaton is a machine that has a finite number of states. Any Two Automaton is said to be equivalent if both accept exactly the same set of input strings.  Two Automaton are equivalent if they satisfy the following conditions :  1. The initial and final states of both the automatons must be same. 2. Every pair of states chosen is from a different automaton only. 3. While combining the states with the input alphabets, the pair results must be either both final states or intermediate states.(i.e both should lie either in the final state or in the non-final state). 4. If the resultant pair has different types of states, then it will be non-equivalent. (i.e. One lies in the final state and the other lies in the intermediate state). Method The method for comparing two FA’s is explained below − Let M and M1 be the two FA’s and Σ be a set of input strings. Step 1  − Construct a transition table that has pairwise entries (q, q 1 ) where q ∈ M and q 1  ∈ M 1  for eac...
Read more

ARDEN'S THEOREM FOR REGULAR EXPRESSIONS

-
Image
    Identities for Regular Expression:- Given R, P, L, Q as regular expressions, the following identities hold − ∅* = ε ε* = ε RR* = R*R R*R* = R* (R*)* = R* RR* = R*R (PQ)*P =P(QP)* (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)* R + ∅ = ∅ + R = R   (The identity for union) R ε = ε R = R   (The identity for concatenation) ∅ L = L ∅ = ∅   (The annihilator for concatenation) R + R = R   (Idempotent law) L (M + N) = LM + LN   (Left distributive law) (M + N) L = ML + NL   (Right distributive law) ε + RR* = ε + R*R = R* Arden's Theorem:- In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions. Statement  − Let  P  and  Q  be two regular expressions. If  P  does not contain null string, then  R = Q + RP  has a unique solution that is  R = QP* Proof  − R = Q + (Q + RP)P  [After putting the value R = Q + RP] = Q + ...
Read more

PIGEONHOLE PRINCIPLE AND APPLICATIONS OF PUMPING LEMMA

-
Image
  Pigeonhole principle for regular language:- a hole or small recess for pigeons to nest a small open compartment (as in a desk or cabinet) for keeping letters or documents a neat category which usu. fails to reflect actual complexities. pigeonhole principle:   if  n  objects are put into  m  containers, where  n  >  m , then at least one container must hold more than one object. The pigeonhole can be used to prove that certain infinite languages are not regular. (Remember, any finite language  is  regular.) As we have informally observed, dfas "can't count." This can be shown formally by using the pigeonhole principle. As an example , we show that L = {a b :  n  > 0} is not regular. The proof is by contradiction. Suppose L is regular. There are an infinite number of values of  n  but M(L) has only a finite number of states. By the pigeonhole principle, there must be distinct values of  i  and...
Read more