ARDEN'S THEOREM FOR REGULAR EXPRESSIONS

-

  Identities for Regular Expression:-

Given R, P, L, Q as regular expressions, the following identities hold −

  • ∅* = ε
  • ε* = ε
  • RR* = R*R
  • R*R* = R*
  • (R*)* = R*
  • RR* = R*R
  • (PQ)*P =P(QP)*
  • (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
  • R + ∅ = ∅ + R = R (The identity for union)
  • R ε = ε R = R (The identity for concatenation)
  • ∅ L = L ∅ = ∅ (The annihilator for concatenation)
  • R + R = R (Idempotent law)
  • L (M + N) = LM + LN (Left distributive law)
  • (M + N) L = ML + NL (Right distributive law)
  • ε + RR* = ε + R*R = R*
Arden's Theorem:-

In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.

Statement −

Let P and Q be two regular expressions.

If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*

Proof −

R = Q + (Q + RP)P [After putting the value R = Q + RP]

= Q + QP + RPP

When we put the value of R recursively again and again, we get the following equation −

R = Q + QP + QP2 + QP3…..

R = Q (ε + P + P2 + P3 + …. )

R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]

Hence, proved.
Assumptions for Applying Arden’s Theorem

  • The transition diagram must not have NULL transitions
  • It must have only one initial state

Method

Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.

q1 = q1R11 + q2R21 + … + qnRn1 + ε

q2 = q1R12 + q2R22 + … + qnRn2

…………………………

…………………………

…………………………

…………………………

qn = q1R1n + q2R2n + … + qnRnn

Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅

Step 2 − Solve these equations to get the equation for the final state in terms of Rij

EXAMPLE:-

Construct a regular expression corresponding to the automata given below −

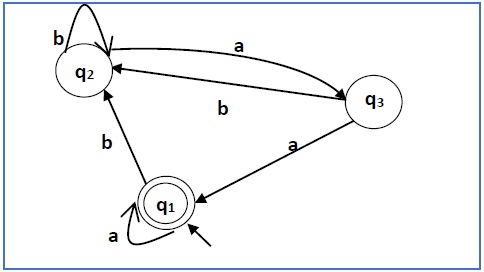
Finite Automata

Solution −

Here the initial state and final state is q1.

The equations for the three states q1, q2, and q3 are as follows −

q1 = q1a + q3a + ε (ε move is because q1 is the initial state0

q2 = q1b + q2b + q3b

q3 = q2a

Now, we will solve these three equations −

q2 = q1b + q2b + q3b

= q1b + q2b + (q2a)b (Substituting value of q3)

= q1b + q2(b + ab)

= q1b (b + ab)* (Applying Arden’s Theorem)

q1 = q1a + q3a + ε

= q1a + q2aa + ε (Substituting value of q3)

= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)

= q1(a + b(b + ab)*aa) + ε

= ε (a+ b(b + ab)*aa)*

= (a + b(b + ab)*aa)*

Hence, the regular expression is (a + b(b + ab)*aa)*.

Comments

Post a Comment

Popular posts from this blog

PIGEONHOLE PRINCIPLE AND APPLICATIONS OF PUMPING LEMMA

-
Image
  Pigeonhole principle for regular language:- a hole or small recess for pigeons to nest a small open compartment (as in a desk or cabinet) for keeping letters or documents a neat category which usu. fails to reflect actual complexities. pigeonhole principle:   if  n  objects are put into  m  containers, where  n  >  m , then at least one container must hold more than one object. The pigeonhole can be used to prove that certain infinite languages are not regular. (Remember, any finite language  is  regular.) As we have informally observed, dfas "can't count." This can be shown formally by using the pigeonhole principle. As an example , we show that L = {a b :  n  > 0} is not regular. The proof is by contradiction. Suppose L is regular. There are an infinite number of values of  n  but M(L) has only a finite number of states. By the pigeonhole principle, there must be distinct values of  i  and  j  such that a i  and a j  end in the same state. From this state, b i  
Read more

EQUIVALENCE OF TWO FINITE AUTOMATAs

-
Image
An Automaton is a machine that has a finite number of states. Any Two Automaton is said to be equivalent if both accept exactly the same set of input strings.  Two Automaton are equivalent if they satisfy the following conditions :  1. The initial and final states of both the automatons must be same. 2. Every pair of states chosen is from a different automaton only. 3. While combining the states with the input alphabets, the pair results must be either both final states or intermediate states.(i.e both should lie either in the final state or in the non-final state). 4. If the resultant pair has different types of states, then it will be non-equivalent. (i.e. One lies in the final state and the other lies in the intermediate state). Method The method for comparing two FA’s is explained below − Let M and M1 be the two FA’s and Σ be a set of input strings. Step 1  − Construct a transition table that has pairwise entries (q, q 1 ) where q ∈ M and q 1  ∈ M 1  for each input symbol. Step 2  
Read more