An Automaton is a machine that has a finite number of states. Any Two Automaton is said to be equivalent if both accept exactly the same set of input strings.
Two Automaton are equivalent if they satisfy the following conditions : 1. The initial and final states of both the automatons must be same.
2. Every pair of states chosen is from a different automaton only.
3. While combining the states with the input alphabets, the pair results must be either both final states or intermediate states.(i.e both should lie either in the final state or in the non-final state).
4. If the resultant pair has different types of states, then it will be non-equivalent. (i.e. One lies in the final state and the other lies in the intermediate state).
Method
The method for comparing two FA’s is explained below −
Let M and M1 be the two FA’s and Σ be a set of input strings.
Step 1 − Construct a transition table that has pairwise entries (q, q1) where q ∈ M and q1 ∈ M1 for each input symbol.
Step 2 − If we get in a pair as one final state and other non-final state then we terminate the construction of transition table declaring that two FA’s are not equivalent
Step 3 − The construction of the transition table gets terminated when there is no new pair appearing in the transition table.
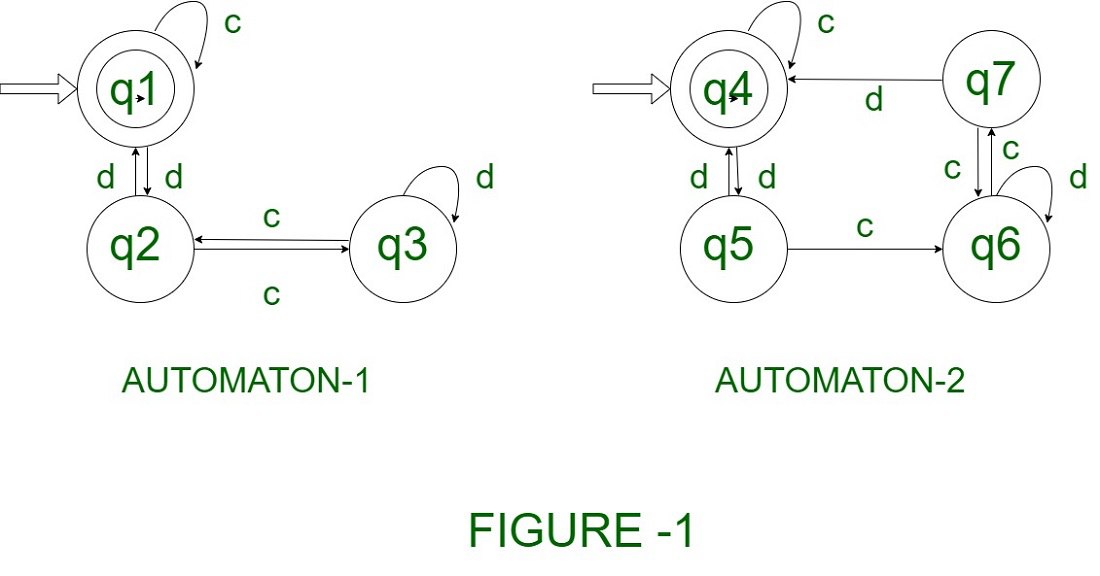
Example 1.
Consider the two Deterministic Finite Automata (DFA) and check whether they are equivalent or not.


Explanation
- Step 1 − First, construct the transition table for each input c and d.
- Step 2 − From the first machine M on receiving input c in state q1, we reach state q1 only which is the final state.
- Step 3 − From the second machine M1 for state q4 on receiving input c, we reach state q4 which is the final state.
- Step 4 − Thus for state (q1, q4) for input c, we get the next states as (q1, q4). Both are final states.
- Step 5 − Similarly, for input d in state (q1, q4), we get the next state as (q2, q5). Both are intermediate states. So, the first state in both machines is equal.
- Step 6 − Similarly, we perform the remaining states in two machines.
- Step 7 − In a pair of states, if both are final or if both are non-final, then we can say that two DFA’s are equivalent and let’s check for remaining.
The transition table is as follows −
| States | c | d |
|---|
| {q1,q4} | {q1, q4}
FS FS
| {q2, q5}
IS IS
|
| {q2,q5} | {q3, q6}
IS IS
| {q1, q4}
FS FS
|
| {q3, q6} | {q2, q7}
IS IS
| {q3, q6}
IS IS
|
| {q2, q7} | {q3, q6}
IS IS
| {q1, q4}
FS FS
|
Here, FS is the Final State and IS is the Intermediate State.
Therefore, by seeing the above table it is clear that we don’t get one final and one intermediate in any pair. Hence, we can declare that two DFA’s are equivalent.
Example 2.
Consider Two Different Automaton shown below in Figure 1.Consider Two Different Automaton shown below in Figure 1.
Solution –
Step 1 – Since the initial and final states of both the automaton are the same, so it verifies.
Step 2 – Check for each state by making a table of states with respect to input alphabets.

Here ,
F.S represents -> Final State.
I.S represents -> Intermediate State (Non-Final State) .
Step 3 – For every pair of states, the resultant states lie either in F.S or in I.S as a combination.
Conclusion – Both the Automaton are equivalent.



Comments
Post a Comment