PIGEONHOLE PRINCIPLE AND APPLICATIONS OF PUMPING LEMMA

 

Pigeonhole principle for regular language:-

1. a hole or small recess for pigeons to nest
2. a small open compartment (as in a desk or cabinet) for keeping letters or documents
3. a neat category which usu. fails to reflect actual complexities.

pigeonhole principle: if n objects are put into m containers, where n > m, then at least one container must hold more than one object.

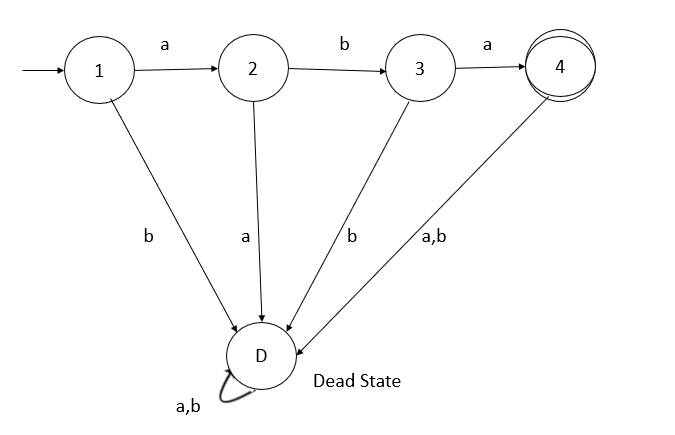
The pigeonhole can be used to prove that certain infinite languages are not regular. (Remember, any finite language is regular.)

As we have informally observed, dfas "can't count." This can be shown formally by using the pigeonhole principle. As an example, we show that L = {ab: n > 0} is not regular. The proof is by contradiction.

Suppose L is regular. There are an infinite number of values of n but M(L) has only a finite number of states. By the pigeonhole principle, there must be distinct values of i and j such that aⁱ and a^j end in the same state. From this state,

• bⁱ must end in a final state, because aⁱbⁱ is in L; and
• bⁱ must end in a nonfinal state, because a^jbⁱ is not in L.

Since the state reached cannot be both final and nonfinal, we have a contradiction. Thus our assumption, that L is regular, must be incorrect.

Application of pumping lemma:-

Proving a language non regular

Consider language L

-> For each n, we propose a word w in L longer than n. 

-> We define parameterized word x and non-empty word y such that 

          - xyz = w for some z and 

          - parameter space covers all x and y such that |xy| ≤ n.

-> For each split x and y, we choose a k such that xy k z 6∈ L. We have proven that L is not regular. 

 Kleene's theorem:-

Kleene's Theorem states the equivalence of the following three statements −

• A language accepted by Finite Automata can also be accepted by a Transition graph.

• A language accepted by a Transition graph can also be accepted by Regular Expression.

• A language accepted by Regular Expression can also be accepted by finite Automata.

Kleene’s theorem proof part-1

A language accepted by Finite Automata can also be accepted by a Transition graph.

Consider an example Let L=aba over an alphabet {a,b}

Third part of Kleene’s theorem

A language accepted by Regular Expression can also be accepted by finite Automata.

Theorem

Any language that can be defined with RE can be accepted by some Finite State Machine (FSM) is also regular.

Proof

The proof is by construction.

For a given RE α, we can construct a FSM M such that

L (α) = L (M)

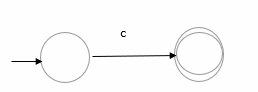
• If α is any c € Σ, we can construct a simple FSM as follows −

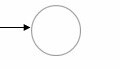
• If α is φ, we construct simple FSM as follows −

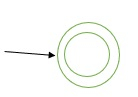
• If α is €, we construct simple FSM as −

• 

• Let us construct FSMs to accept language that are defined by regular expression that exploits the operations of concatenation, union and Kleene star.

  Step 1

  Let β and γ be RE that defined languages over the alphabet Σ

  If L(β) is regular, then it is accepted by some FSM

  M1 = (Q1, Σ, δ1, q1, F1)

  Let L(γ) is regular, then it is accepted by some FSM

  M2= (Q2, Σ, δ2, q2, F2)

  Step 2

  If RE α= β ∪ γ and if both L(β) and L(γ) are regular,

  Then we construct M3=( Q3, Σ, δ3, q3, F3), such that

  L(M3)=L(α)=L(β) ∪ L(γ)

  Step 3

  Let P accept L = {a} and Q accepts L = {b}, then R can be represented as a combination of P and Q by using the provided operations as −

  R = P+ Q

  The transition diagram for the same is given below −

  

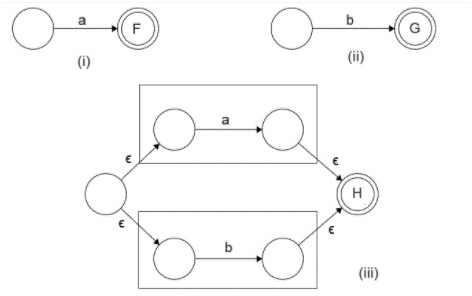
  We observe the following in the transition diagram −

  • In case of union operation we can have a new start state. From there, a null transition proceeds to the starting state of both the Finite State Machines.

  • The final states of both the Finite Automata are converted to intermediate states. The final state is unified into one which can be traversed by null transitions