ARDEN'S THEOREM FOR REGULAR EXPRESSIONS

-
Image
    Identities for Regular Expression:- Given R, P, L, Q as regular expressions, the following identities hold − ∅* = ε ε* = ε RR* = R*R R*R* = R* (R*)* = R* RR* = R*R (PQ)*P =P(QP)* (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)* R + ∅ = ∅ + R = R   (The identity for union) R ε = ε R = R   (The identity for concatenation) ∅ L = L ∅ = ∅   (The annihilator for concatenation) R + R = R   (Idempotent law) L (M + N) = LM + LN   (Left distributive law) (M + N) L = ML + NL   (Right distributive law) ε + RR* = ε + R*R = R* Arden's Theorem:- In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions. Statement  − Let  P  and  Q  be two regular expressions. If  P  does not contain null string, then  R = Q + RP  has a unique solution that is  R = QP* Proof  − R = Q + (Q + RP)P  [After putting the value R = Q + RP] = Q + ...
Post a Comment

N.D.F.A TO D.F.A. CONVERSION

-
 Difference between D.F.A. and N.D.F.
Each transition leads to exactly one state called as deterministicA transition leads to a subset of states i.e. some transitions can be non-deterministic.
Accepts input if the last state is in FinalAccepts input if one of the last states is in Final.
Backtracking is allowed in DFA.Backtracking is not always possible.
Requires more space.Requires less space.
Empty string transitions are not seen in DFA.Permits empty string transition.
For a given state, on a given input we reach a deterministic and unique state.For a given state, on a given input we reach more than one state.
DFA is a subset of NFA.Need to convert NFA to DFA in the design of a compiler.
δ : Q × Σ → Q
For example − δ(q0,a)={q1}
δ : Q × Σ → 2Q
For example − δ(q0,a)={q1,q2}
DFA is more difficult to construct.NFA is easier to construct.
DFA is understood as one machine.
NFA is understood as multiple small machines computing at the same time.


Steps for converting N.D.F.A. to D.F.A. :-

Step 1: Initially Q' = ϕ

Step 2: Add q0 of NFA to Q'. Then find the transitions from this start state

Step 3: In Q', find the possible set of states for each input symbol. If this set of states is not in Q', then add it to Q'.

Step 4: In DFA, the final state will be all the states which contain F(final states of NFA)

Examples:-
1. Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA)-

 

--> Transition table for the given Non-Deterministic Finite Automata (NFA) is-
State / Alphabetab
→q0q0q0, q1
q1–*q2
*q2––

Step-01:

 

Let Q’ be a new set of states of the Deterministic Finite Automata (DFA).

Let T’ be a new transition table of the DFA.

 

Step-02:

 

Add transitions of start state q0 to the transition table T’.

 

State / Alphabetab
→q0q0{q0, q1}

 

Step-03:

New state present in state Q’ is {q0, q1}.

Add transitions for set of states {q0, q1} to the transition table T’.

 

State / Alphabetab
→q0q0{q0, q1}
{q0, q1}q0{q0, q1, q2}

 

Step-04:

 

New state present in state Q’ is {q0, q1, q2}.

Add transitions for set of states {q0, q1, q2} to the transition table T’.

State / Alphabetab
→q0q0{q0, q1}
{q0, q1}q0{q0, q1, q2}
{q0, q1, q2}q0{q0, q1, q2}

 

Step-05:

 

Since no new states are left to be added in the transition table T’, so we stop.

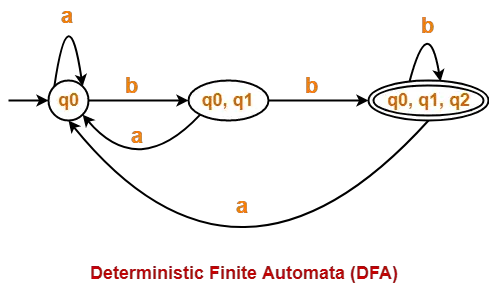
States containing q2 as its component are treated as final states of the DFA.

 

Finally, Transition table for Deterministic Finite Automata (DFA) is-

 

State / Alphabetab
→q0q0{q0, q1}
{q0, q1}q0*{q0, q1, q2}
*{q0, q1, q2}q0*{q0, q1, q2}

 

Now, Deterministic Finite Automata (DFA) may be drawn as-

 

Comments

Post a Comment

Popular posts from this blog

PIGEONHOLE PRINCIPLE AND APPLICATIONS OF PUMPING LEMMA

-
Image
  Pigeonhole principle for regular language:- a hole or small recess for pigeons to nest a small open compartment (as in a desk or cabinet) for keeping letters or documents a neat category which usu. fails to reflect actual complexities. pigeonhole principle:   if  n  objects are put into  m  containers, where  n  >  m , then at least one container must hold more than one object. The pigeonhole can be used to prove that certain infinite languages are not regular. (Remember, any finite language  is  regular.) As we have informally observed, dfas "can't count." This can be shown formally by using the pigeonhole principle. As an example , we show that L = {a b :  n  > 0} is not regular. The proof is by contradiction. Suppose L is regular. There are an infinite number of values of  n  but M(L) has only a finite number of states. By the pigeonhole principle, there must be distinct values of  i  and...
Read more

ARDEN'S THEOREM FOR REGULAR EXPRESSIONS

-
Image
    Identities for Regular Expression:- Given R, P, L, Q as regular expressions, the following identities hold − ∅* = ε ε* = ε RR* = R*R R*R* = R* (R*)* = R* RR* = R*R (PQ)*P =P(QP)* (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)* R + ∅ = ∅ + R = R   (The identity for union) R ε = ε R = R   (The identity for concatenation) ∅ L = L ∅ = ∅   (The annihilator for concatenation) R + R = R   (Idempotent law) L (M + N) = LM + LN   (Left distributive law) (M + N) L = ML + NL   (Right distributive law) ε + RR* = ε + R*R = R* Arden's Theorem:- In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions. Statement  − Let  P  and  Q  be two regular expressions. If  P  does not contain null string, then  R = Q + RP  has a unique solution that is  R = QP* Proof  − R = Q + (Q + RP)P  [After putting the value R = Q + RP] = Q + ...
Read more

EQUIVALENCE OF TWO FINITE AUTOMATAs

-
Image
An Automaton is a machine that has a finite number of states. Any Two Automaton is said to be equivalent if both accept exactly the same set of input strings.  Two Automaton are equivalent if they satisfy the following conditions :  1. The initial and final states of both the automatons must be same. 2. Every pair of states chosen is from a different automaton only. 3. While combining the states with the input alphabets, the pair results must be either both final states or intermediate states.(i.e both should lie either in the final state or in the non-final state). 4. If the resultant pair has different types of states, then it will be non-equivalent. (i.e. One lies in the final state and the other lies in the intermediate state). Method The method for comparing two FA’s is explained below − Let M and M1 be the two FA’s and Σ be a set of input strings. Step 1  − Construct a transition table that has pairwise entries (q, q 1 ) where q ∈ M and q 1  ∈ M 1  for eac...
Read more