ARDEN'S THEOREM FOR REGULAR EXPRESSIONS
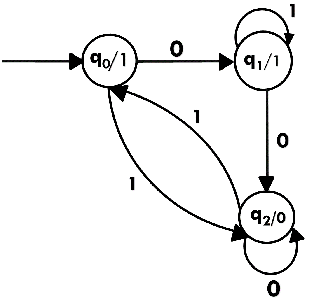
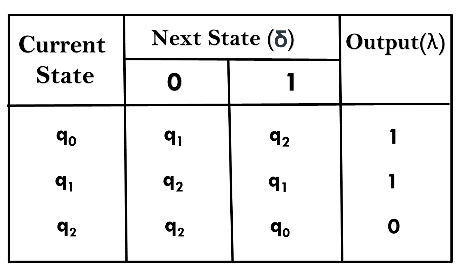
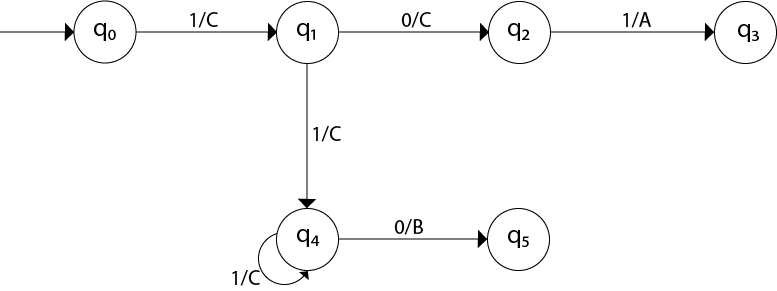
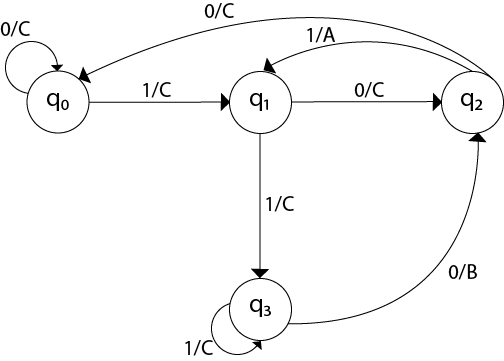
Identities for Regular Expression:- Given R, P, L, Q as regular expressions, the following identities hold − ∅* = ε ε* = ε RR* = R*R R*R* = R* (R*)* = R* RR* = R*R (PQ)*P =P(QP)* (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)* R + ∅ = ∅ + R = R (The identity for union) R ε = ε R = R (The identity for concatenation) ∅ L = L ∅ = ∅ (The annihilator for concatenation) R + R = R (Idempotent law) L (M + N) = LM + LN (Left distributive law) (M + N) L = ML + NL (Right distributive law) ε + RR* = ε + R*R = R* Arden's Theorem:- In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions. Statement − Let P and Q be two regular expressions. If P does not contain null string, then R = Q + RP has a unique solution that is R = QP* Proof − R = Q + (Q + RP)P [After putting the value R = Q + RP] = Q + ...
Comments
Post a Comment