MINIMIZATION OF D.F.A.

 ->In automata theory (a branch of theoretical computer science), DFA minimization is the task of transforming a given deterministic finite automaton (DFA) into an equivalent DFA that has a minimum number of states. Here, two DFAs are called equivalent if they recognize the same regular language. Several different algorithms accomplishing this task are known and described in standard textbooks on automata theory.

->Minimal D.F.A. - For each regular language, there also exists a minimal automaton that accepts it, that is, a DFA with a minimum number of states and this DFA is unique (except that states can be given different names). The minimal DFA ensures minimal computational cost for tasks such as pattern matching.

There are two classes of states that can be removed or merged from the original DFA without affecting the language it accepts.

->Unreachable states are the states that are not reachable from the initial state of the DFA, for any input string. These states can be removed.
->Dead states are the states from which no final state is reachable. These states can be removed unless the automaton is required to be complete.
->Nondistinguishable states are those that cannot be distinguished from one another for any input string. These states can be merged.

DFA minimization is usually done in three steps:

1. remove dead and unreachable states (this will accelerate the following step),
2. merge nondistinguishable states,
3. optionally, re-create a single dead state ("sink" state) if the resulting DFA is required to be complete.   

->Minimization using Equivalence Theorem:- If X and Y are two states in a DFA, we can combine these two states into {X, Y} if they are not distinguishable. Two states are distinguishable, if there is at least one string S, such that one of δ (X, S) and δ (Y, S) is accepting and another is not accepting. Hence, a DFA is minimal if and only if all the states are distinguishable.

Step 1 − All the states Q are divided in two partitions − final states and non-final states and are denoted by P0. All the states in a partition are 0th equivalent. Take a counter k and initialize it with 0.

Step 2 − Increment k by 1. For each partition in Pk, divide the states in Pk into two partitions if they are k-distinguishable. Two states within this partition X and Y are k-distinguishable if there is an input S such that δ(X, S) and δ(Y, S) are (k-1)-distinguishable.

Step 3 − If Pk ≠ Pk-1, repeat Step 2, otherwise go to Step 4.

Step 4 − Combine kth equivalent sets and make them the new states of the reduced DFA.

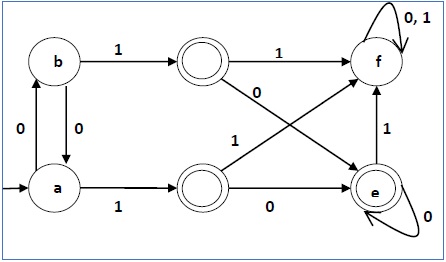
Example

Let us consider the following DFA −

q	δ(q,0)	δ(q,1)
a	b	c
b	a	d
c	e	f
d	e	f
e	e	f
f	f	f

Let us apply the above algorithm to the above DFA −

• P0 = {(c,d,e), (a,b,f)}
• P1 = {(c,d,e), (a,b),(f)}
• P2 = {(c,d,e), (a,b),(f)}

Hence, P1 = P2.

There are three states in the reduced DFA. The reduced DFA is as follows −

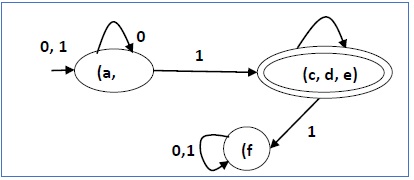
Q	δ(q,0)	δ(q,1)
(a, b)	(a, b)	(c,d,e)
(c,d,e)	(c,d,e)	(f)
(f)	(f)	(f)